Introduction to X-ray Diffraction

Introduction

X—ray diffraction is a non-destructive technique that utilizes elastic scattering to determine atomic structural information about crystalline samples. It requires high energy hard x-rays, as they have an extremely small wavelength, to discern details on the atomic level. It is a technique widely used for the identification and characterization of unknown crystalline materials, which is critical for applications such as geology, material science, and biology.

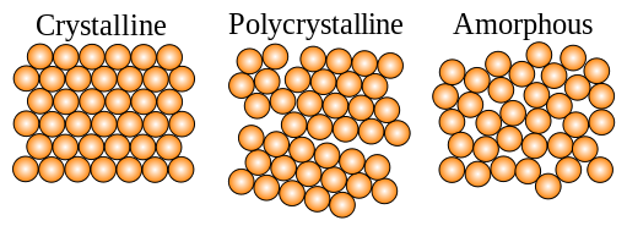
Crystalline structures are defined as any structure of ions, atoms, or molecules that form in an ordered, three-dimensional arrangement. As the ions, atoms, or molecules are regularly spaced, they act as a three-dimensional grating. When a monochromatic x-ray beam interacts with this ordered structure, constructive interference occurs. By measuring this constructive interference, information about the repeating atomic structure or interfaces in multilayer materials can be established.

Figure 1: Schematic of a crystalline structure, showing ordered regular spacing of the atoms, ions, or molecules, a polycrystalline structure, showing multiple crystallites of regular spacing, all which have different orientation and size, and an amorphous structure, in which the atoms, ions, or molecules have random order and spacing.

X-ray diffraction is determined by Braggs law, which is defined as nλ = 2dsinθ.  This law relates wavelength to diffraction angle and the atomic spacing of the lattice within a crystalline sample (known as d-spacing). By using a fixed wavelength (i.e. monochromatic x-ray) the d-spacing can be determined for a specific angle. Rotating either the sample or the detector through a full range of angles allows for the full profile of the material to be measured.

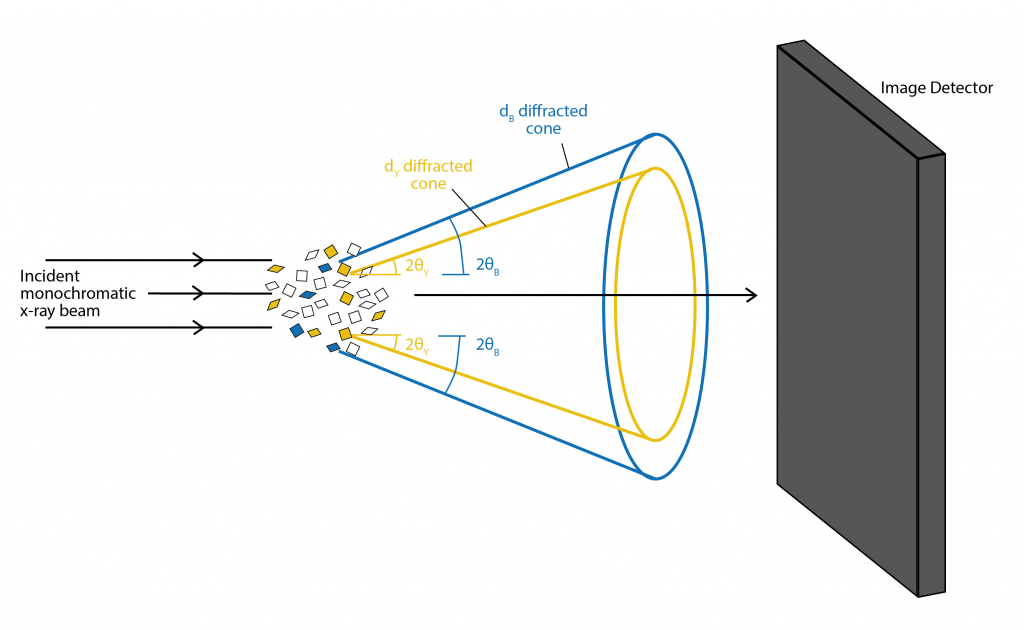
There are two main types of diffraction experiments, powder diffraction and single crystal diffraction. Powder diffraction is used to study polycrystalline samples. By illuminating the powder with a monochromatic x-ray beam, each d-spacing and a fixed angle θ will produce a cone of diffracted x-rays. The image detector records the cone of diffracted x-rays as a ring. D-spacing can be calculated by fitting the peak intensity of the angle around the ring against the angle θ. This is typically done via software. For powder diffraction it is essential that the sample is measured over the full range of angles to get a full profile, as the powdered material will have random orientation of the crystal lattice. Chemical information about the powder can also be determined by comparing the d-spacing profile to known reference profiles.

Figure 2: Schematic of how powder diffraction causes a cone of diffracted x-rays which are recorded as a ring on an image detector. Each crystallite of regular spacing produces a different diffraction cone which allows for the sample to be identified and characterized.

Single crystal diffraction is one of the oldest and most precise diffraction methods. It also utilizes a monochromatic x-ray to get the lattice structure of single crystals. The diffraction of x-rays in the single crystal produces a 3D array of spots that is recorded by the image plate. The spots that are visible will come from a limited number of lattice planes, known as a zone. By rotating either the crystal or the detector, every zone can be measured, and the entire crystal structure can be derived.

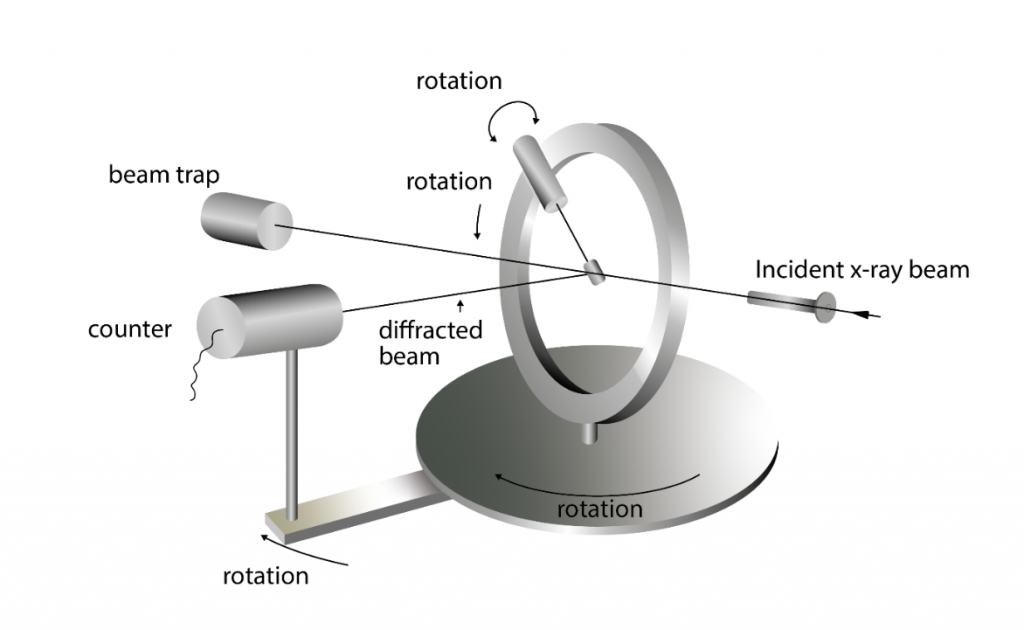
Figure 3: Schematic of a typical 4-circle diffractometer used to conduct single crystal diffraction. The diffractometer has 4 different sections of rotation to obtain the full structural profile.

Single crystal diffraction can also be used to determine the complete structure of a mineral. Scattering power of the atoms depends on the density of the atoms in the lattice, the atomic number, and the intensity of x-rays in each reflection. These parameters are required to find the position of each atom within the unit cell. Therefore, with sufficient quality data the complete mineral structure can be determined from a monochromatic x-ray beam.

White light (i.e. multiple x-ray wavelengths) can also be used for single crystal diffraction. Instead of a 3D array of spots, the diffracted light is elongated and is referred to as a “pencil”. The Bragg condition is satisfied at different wavelengths down the length of the pencil. Although angles of diffraction can be determined, it cannot be determined which elongated spots relate to which angle and wavelength pair, preventing d-spacing from being calculated. To overcome this, the detector position needs to be calibrated, and a comparison of the angles between the spots and the angles between diffraction directions. In this way the crystal structure and orientation of the crystal can be determined.