Pixel Size and Camera ResolutionEducational Notes

Pixel Size

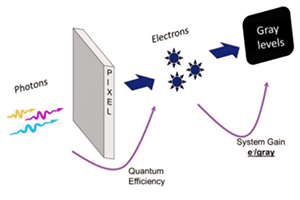
A pixel is the part of a sensor which collects photons so they can be converted into photoelectrons. Multiple pixels cover the surface of the sensor so that both the number of photons detected, and the location of these photons can be determined.

Pixels come in many different sizes, each having their advantages and disadvantages. Larger pixels are able to collect more photons, due to their increase in surface area. This allows more photons to be converted into photoelectrons, increasing the sensitivity of the sensor. However, this is at the cost of resolution.

Smaller pixels are able to provide higher spatial resolution but capture less photons per pixel. To try and overcome this, sensors can be back-illuminated to maximize the amount of light being captured and converted by each pixel.  

The size of the pixel also determines the overall size of the sensor. For example, a sensor which has 1024 x 1024 pixels, each with a 169 μm² surface area, results in a sensor size of 13.3 x 13.3 mm. Yet, a sensor with the same number of pixels, now with a 42.25 μm² surface area, results in a sensor size of 6.7 x 6.7 mm.

Camera Resolution

Camera resolution is the ability of the imaging device to resolve two point that are close together. The higher the resolution, the smaller the detail that can be resolved from an object. It is influenced by pixel size, magnification, camera optics and the Nyquist limit. Camera resolution can be determined by the equation:

Where 2.3 compensates for the Nyquist limit. This limit is determined by the Rayleigh Criterion of the sample. The Rayleigh Criterion is defined by whether or not two neighboring Airy disks (central bright spot of the diffraction pattern from a light source) can be distinguished from one another, determining the smallest point that can be resolved (as shown in Figure 1).

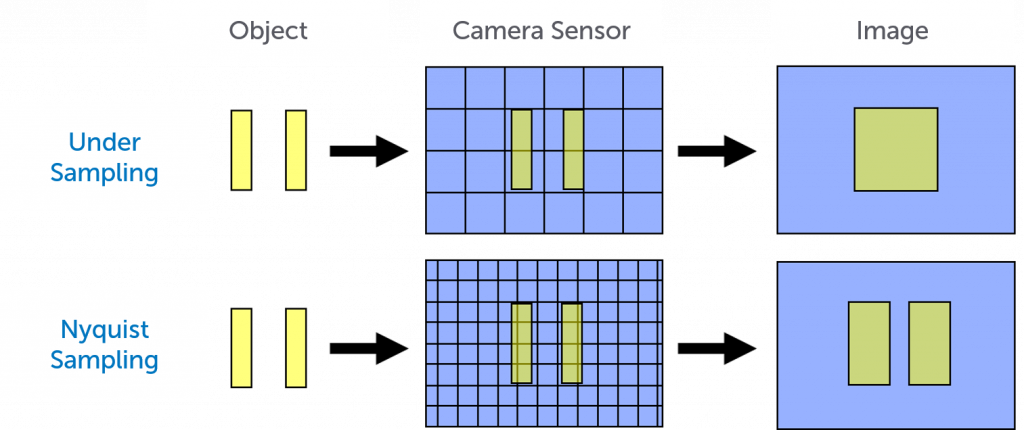
Nyquist limit determines whether a sensor can differentiate between two neighboring objects. If the distance between two objects is greater than the Nyquist limit, or exceed this limit by a factor of at least 2, a sensor can distinguish between the two objects. The Nyquist limit is determined by the spatial frequency (number of bright spots within a given distance) of the object you are trying to image.

For example, if you are trying to measure a few bright spots that are α nm apart, you will need to measure at least every  nm to capture the spatial frequency (i.e. resolve the bright spots). This spatial frequency allows the gaps between the bright spots to be captured as a black pixel (i.e. a pixel without signal). If the distance between the bright spots is less than the size of the pixel, a black pixel will not be captured and therefore the bright spots will not be resolved. This is why smaller pixels provide higher resolution, as shown in Figure 2.

Lens Resolution

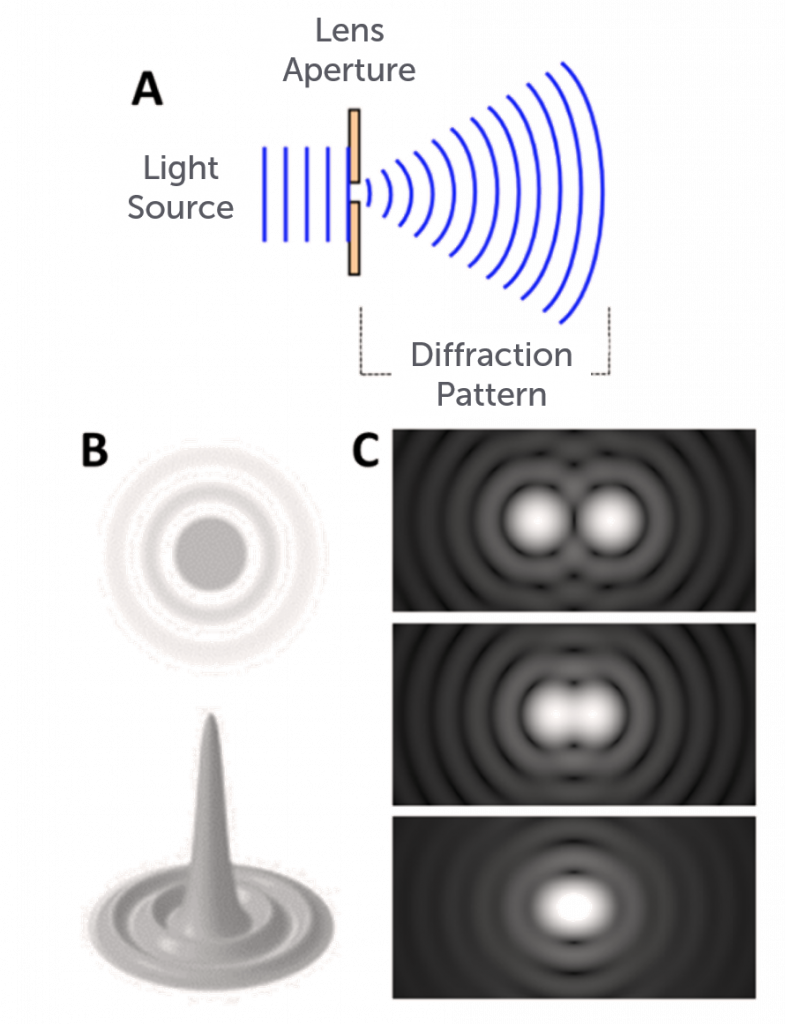
It is also important to consider the resolution of the camera lens when determining the overall system resolution. The ability for a lens to resolve an object is limited by diffraction. When the light emitted from an object travels through a lens aperture it diffracts, forming a diffraction pattern in the image (as shown in Figure 3A). This is known as an Airy pattern, and has a central spot surrounded by bright rings with darker regions in-between (Figure 3B). The central bright spot is called an Airy disk, of which the angular radius is given by:

Where θ is the angular resolution (radians), λ is the wavelength of light (m), and D is the diameter of the lens (m).

Two different points on an object being imaged produce two different Airy patterns. If the angular separation between the two points is greater than the angular radius of their Airy disk, the two objects can be resolved (Rayleigh’s Criterion). If the angular separation is smaller, however, the two distinct points on the object merge. This can be seen in Figure 3C.

The angular radius of the Airy disk is determined by the aperture of the lens; therefore, the diameter of the lens aperture also determines resolution. As the diameter of the lens aperture and the angular radius of the Airy disk have an inverse relationship, the larger the aperture the smaller the angular radius. This means that a larger aperture results in higher lens resolution as the distance between smaller details can remain greater than the angular radius of the Airy disk. This is often why astronomical telescopes have large lens diameters to be able to resolve the finer details in stars.

Summary

Pixels come in various sizes depending on what is required for the application. A large pixel size is optimal for low light imaging conditions that are less concerned with high resolution. In comparison, a smaller pixel size is optimal for bright imaging conditions in which resolving fine detail is of the utmost importance.

The size of the pixel also determines the number of pixels on a sensor, with a fixed sensor size having more pixels on the surface with smaller pixel surface area.

Camera resolution is determined by the pixel size, lens aperture, magnification and Nyquist limit. Overcoming the Nyquist limit is down to the pixel size, with smaller pixels allowing for even smaller details to be resolved. This is because the distance between two neighboring objects needs to be bigger than that of one pixel size, allowing for a black pixel to be captured distinguishing a gap between the two objects.

Lens resolution is limited by diffraction. Airy patterns are formed when light from an object diffracts through a lens aperture. These Airy patterns have bright central spots called Airy disks, which have an angular radius determined by the lens aperture diameter. Two neighboring objects can be resolved if the angular separation between the objects is greater than the angular radius of the Airy disk. As this is inversely related to the aperture diameter, a larger lens aperture results in higher resolution.

Both pixel size and lens aperture diameter need to be taken into consideration when choosing the right camera for a research application.