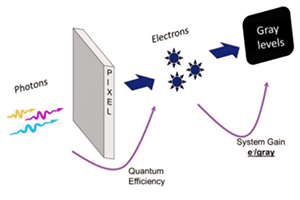
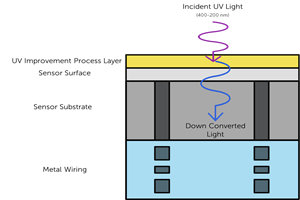
What is FOV and how does it influence your data?

Introduction

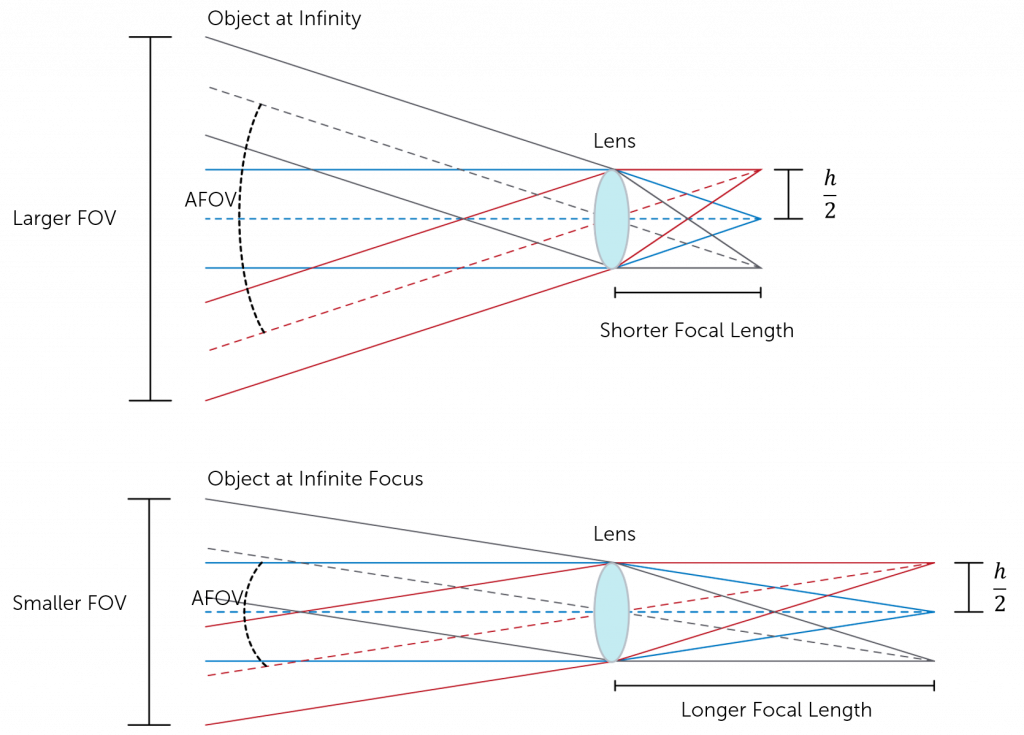
Field of view (FOV) is the maximum area of a sample that a camera can image. It is related to two things, the focal length of the lens and the sensor size. Figure 1 shows a comparison between the field of view and the size of the sensor. Assuming that the focal length of the lens is the same, the larger the sensor the larger the field of view.

Figure 1: Comparison of different sensor sizes, showing how larger sensor sizes contribute to a larger field of view. Both the blue (4096 x 4096 pixels) and red (2048 x 2048 pixels) square indicate sensors made from 15 x 15 μm pixels, whereas the green square (1024 x 1024 pixels) indicates a sensor made from 13 x 13 μm pixels.

The sensor size is determined by both the number of pixels on the sensor, and the size of the pixels. Different sized pixels are used for different applications, with larger pixels used for higher sensitivity, and smaller pixels used for higher spatial resolution (find out more on Pixel Size and Camera Resolution).

The focal length of the lens describes the distance between the lens and the focused image on the sensor. As light passes through the lens it will either converge (positive focal length) or diverge (negative focal length), however within cameras the focal length is predominately positive. Shorter focal lengths converge the light more strongly (i.e. at a sharper angle) to focus the subject being imaged. Longer focal lengths, in comparison, converge the light less strongly (i.e. at a shallower angle) in order to focus the image.

This means that the distance of the focal length is determined by how strongly the light is converged by the lens in order to focus the subject being imaged. This, in turn, influences the angle from the horizonal of light that can be captured by the lens. This is known as the angular field of view (AFOV) and is required to determine the overall FOV. The AFOV is the angle between any light captured at the horizonal, and any light captured at the edge (as shown in Figure 2). If you have a fixed sensor size, altering the focal length will alter the AFOV and therefore the overall FOV. A shorter focal length provides a larger AFOV view, and therefore a larger FOV. The same is true but vice versa for longer focal lengths, as indicated in Figure 2.

Figure 2: Schematic depicting how focal length has an impact on the angular field of view (AFOV). The shorter the focal length, the larger the AFOV, and vice versa for longer focal length. This influences the size of the FOV. Red line indicates light from the bottom of the object, creating the top of the image; blue light is light that is taken from the horizontal; grey lines indicate light that is from the top of the object, creating the bottom of the image. The height of the image is indicated by h.

Calculating AFOV

When calculating AFOV a few assumptions need to be made:

That the object being imaged completely fills the camera sensor
That the lens is at infinity focus (i.e. when an image is formed from an object at infinity away)
The lens is a pinhole

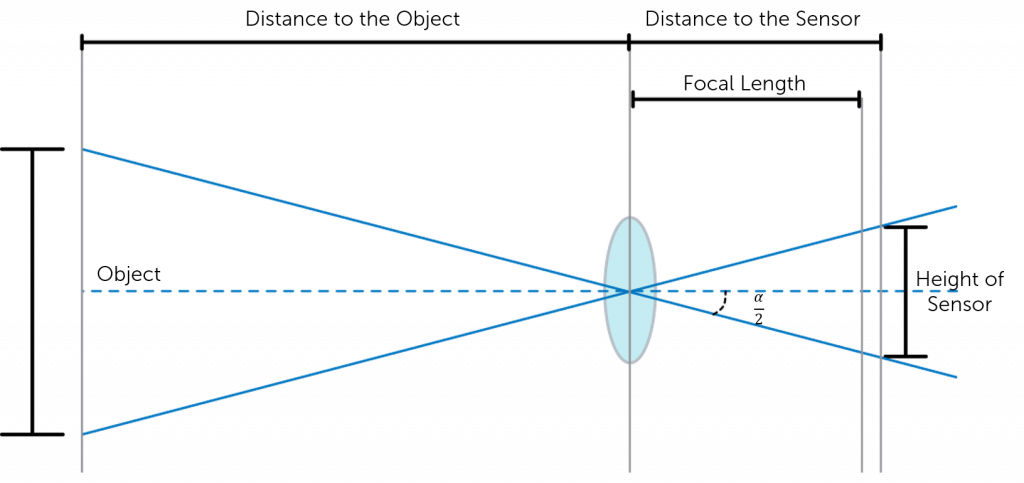
Figure 3: A diagram indicating how the three assumptions can be used to calculate the angular field of view (AFOV). By assuming the lens is a pinhole and at infinity focus, and that the object being imaged fills the sensor, a simple equation can be used to determine the AFOV (in degrees). Refers to the angle of view, as it is the angle which captures the largest object while still fitting the image on the sensor.

Figure 3 shows a simplified version of how these assumptions allow for AFOV calculation. By using trigonometry, the AFOV can be expressed as:

AFOV(°) = {2tan}^{-1} (\frac{h}{2F})

where h is the horizontal dimension of the sensor and F is the focal length of the camera lens.

Measuring FOV

To measure the FOV of UV, visible and infrared cameras, optical tests are commonly used. During the test, light is focused from a black body (an object that absorbs all light that falls on it) onto a test target at the focal place. By using a set of mirrors, a virtual image can be created that is at an infinitely far distance.

This allows the FOV dimensions (i.e. vertical and horizontal distances) to be measured without knowing lens focal length or sensor size. The image created, including the target, is then displayed on a monitor, with the target image being a subset of the full image display. This allows the FOV to be approximated as:

FOV = AOV (\frac{d}{D})

Where D is the full display image dimensions (either horizontal or vertical), and d is the target dimensions (either horizontal or vertical).

Summary

Field of view defines the maximum area of a sample that a camera can image, determined by the focal length of the lens and the sensor size.

Sensor size is determined by both the size of the pixels and number of pixels on the sensor. This can be optimized for each application, with larger sensors optimal for sensitivity limited applications, and smaller sensors optimal for resolution limited applications.

The focal length of a lens converges light so that the image of an object is focused onto the sensor. This determines the angular field of view, a parameter of the overall field of view. This is defined as the angle between any light captured at the horizontal and any light captured at the edge of the of the object. All of these parameters play a role in determining the FOV of a camera and can be measured using either trigonometry and the angular field of view, or via an optical test, in which a black body is utilized to create a virtual image